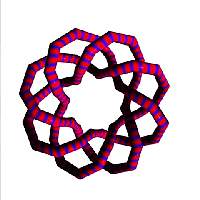
m1=1;m2=2;m3=3;
p=2*PI*u;
q=2*PI*v;
xc=a*sin(m1*p);
yc=b*sin(m2*p);
zc=c*sin(m3*p);
xt=a*m1*cos(m1*p);
yt=b*m2*cos(m2*p);
zt=c*m3*cos(m3*p);
xn=-yt;
yn=xt;
zn=0;
nn=sqrt(pow(xn,2)+pow(yn,2)+pow(zn,2));
xn1=xn/nn;
yn1=yn/nn;
zn1=zn/nn;
xb=-xt*zt;
yb=-yt*zt;
zb=xt*xt+yt*yt;
nb=sqrt(pow(xb,2)+pow(yb,2)+pow(zb,2));
xb1=xb/nb;
yb1=yb/nb;
zb1=zb/nb;
r1=0.5;r2=0.5;
x=xc+r1*cos(q)*xn1+r2*sin(q)*xb1;
y=yc+r1*cos(q)*yn1+r2*sin(q)*yb1;
z=zc+r1*cos(q)*zn1+r2*sin(q)*zb1;
p=2*PI*u;
red=abs(cos(mt*p));
blue=1-red;
green=0;