Accueil Carrara : Index 

 

L'éditeur de formules de Carrara Studio - Page 34

Courbes planes et couleurs (suite 2)

1 : Astroïde et quadrifolium

11 : Astroïde, quadrifolium et cercle

Le quadrifolium a pour équation (x^2 + y^2)^3 - 4*a^2*x^2*y^2 = 0

L'astroïde a pour équation x^(2/3) + y^(2/3) - b^(2/3) = 0

Le cercle a pour équation x^2 + y^2 - b^2 = 0

Formule fond (ou texture) Rendu

a=1;b=2*a;
e1=0.01;e2=0.03;e3=0.01;
pmin=-2.5;pmax=2.5;
qmin=-2.5;qmax=2.5;
p=(pmax-pmin)*u+pmin;
q=(qmax-qmin)*v+qmin;
expr1=pow(p*p+q*q,3)-4*a*a*p*p*q*q;
expr2=p*p+q*q-b*b;
expr3=pow(p*p,1/3)+pow(q*q,1/3)-pow(b*b,1/3);
courbe1=(abs(expr1)<e1);
courbe2=(abs(expr2)<e2);
courbe3=(abs(expr3)<e3);
red=1-courbe1;
blue=1-courbe2;
green=1-courbe3;

 34courbeplane11.jpg

12 : Astroïde en tube

L'astroïde est représentée dans le plan z = cpar la paramétrisation (x = b*pow(cos(t),3) , y = b*pow(sin(t),3) , z = c).

L'équation du tube correspondant est :

x=b*pow(cos(p),3)+r*sin(p)*cos(q);
y=b*pow(sin(p),3)+r*cos(p)*cos(q);
z=c-r*sin(q);

où r est le rayon du tube.

Formule objet Formule texture Rendu

b=5;c=0;r=0.1;
p=2*PI*u;
q=2*PI*v;
x=b*pow(cos(p),3)+r*sin(p)*cos(q);
y=b*pow(sin(p),3)+r*cos(p)*cos(q);
z=c-r*sin(q);

mt=8;
p=2*PI*u;
red=abs(cos(mt*p));
blue=abs(cos(mt*p+2*PI/3));
green=abs(cos(mt*p+4*PI/3));		 34courbeplane12.jpg

13 : Quadrifolium en tube

Le quadrifolium est représenté dans le plan z = c par l'équation polaire rho = a*sin(2 t)

D'où sa paramétrisation spatiale (x = rho*cos(t) , y = rho*sin(t) , z = c).

L'équation du tube correspondant est :

où r est le rayon du tube.

Formule objet Formule texture Rendu

a=5;c=0;r=0.1;
p=2*PI*u;
q=2*PI*v;
s=sqrt(10+6*cos(4*p));
x=2*a*pow(cos(p),2)*sin(p)+r*cos(q)*(sin(p)-3*sin(3*p))/s;
y=2*a*pow(sin(p),2)*cos(p)+r*cos(q)*(cos(p)+3*cos(3*p))/s;
z=c+r*sin(q);

 mt=8;
p=2*PI*u;
red=abs(cos(mt*p));
blue=abs(cos(mt*p+2*PI/3));
green=abs(cos(mt*p+4*PI/3));		 34courbeplane13.jpg

2 : Deltoïde et trifolium

21 : Deltoïde, trifolium et cercle

Le trifolium a pour équation, après rotation de centre l'origine du repère et d'angle PI/4, (X^2 + Y^2)^2 - a*X*(X^2 - 3*Y^2) = 0 où

X = sqrt(2)*(x+y)/2 et Y = sqrt(2)*(x-y)/2

La deltoïde a pour équation (x^2 + y^2)^2 - 8*a*x*(x^2 - 3*y^2) + 18*a^2*(x^2 + y^2) - 27*a^4 = 0

Le cercle a pour équation x^2 + y^2 - a^2 = 0

Formule fond (ou texture) Rendu
a=2;
e1=0.1;e2=0.1;e3=5;
pmin=-4;pmax=8;
qmin=-6;qmax=6;
p=(pmax-pmin)*u+pmin;
q=(qmax-qmin)*v+qmin;
pr=(p+sqrt(3)*q)/2;
qr=(-sqrt(3)*p+q)/2;
expr1=pow(pr*pr+qr*qr,2)-a*pr*(pr*pr-3*qr*qr);
expr2=p*p+q*q-a*a;
expr3=pow(p*p+q*q,2)-8*a*p*(p*p-3*q*q)+18*a*a*(p*p+q*q)-27*pow(a,4);
courbe1=(abs(expr1)<e1);
courbe2=(abs(expr2)<e2);
courbe3=(abs(expr3)<e3);
red=1-courbe1;
blue=1-courbe2;
green=1-courbe3;
 34courbeplane21.jpg

23 : Trifolium en tube

Le trifolium est représenté dans le plan z = cpar l'équation polaire rho = a*cos(3*t).

D'où sa paramétrisation spatiale (x = rho*cos(t) , y = rho*sin(t) , z = c).

L'équation du tube correspondant est :

où r est le rayon du tube.

Formule objet Formule texture Rendu

a=5;c=0;r=0.1;
p=2*PI*u;
q=2*PI*v;
s=sqrt(5-4*cos(6*p));
x=0.5*(a*(cos(2*p)+cos(4*p))+2*r*(cos(2*p)-2*cos(4*p))*cos(q)/s);
y=0.5*(a*(2*cos(2*p)-1)-2*r*(1+4*cos(2*p))*cos(q)/s)*sin(2*p);
z=c+r*sin(q);

 mt=8;
p=2*PI*u;
red=abs(cos(mt*p));
blue=abs(cos(mt*p+2*PI/3));
green=abs(cos(mt*p+4*PI/3));		 34courbeplane23.jpg

3 : Conchale

31 : Neuf conchales

La conchale a pour équation habituelle ((x - a)^2 + y^2)(x + a )^2 - c^4 = 0.

Après rotation de centre l'origine du repère et d'angle PI/2, l'équation devient ((y - a)^2 + x^2)(y + a )^2 - c^4 = 0

Formule fond (ou texture) Rendu

a=1;
c1=0.6*a;c2=0.7*a;c3=0.8*a;c4=0.9*a;c5=a;c6=1.1*a;c7=1.2*a;c8=1.3*a;c9=1.4*a;
e1=0.1;e2=0.1;e3=0.05;e4=0.1;e5=0.1;e6=0.1;e7=0.1;e8=0.1;e9=0.1;
pmin=-5;pmax=5;
qmin=-5;qmax=5;
p=(pmax-pmin)*u+pmin;
q=(qmax-qmin)*v+qmin;
expr1=(pow(q-a,2)+pow(p,2))*pow(q+a,2)-pow(c1,4);
expr2=(pow(q-a,2)+pow(p,2))*pow(q+a,2)-pow(c2,4);
expr3=(pow(q-a,2)+pow(p,2))*pow(q+a,2)-pow(c3,4);
expr4=(pow(q-a,2)+pow(p,2))*pow(q+a,2)-pow(c4,4);
expr5=(pow(q-a,2)+pow(p,2))*pow(q+a,2)-pow(c5,4);
expr6=(pow(q-a,2)+pow(p,2))*pow(q+a,2)-pow(c6,4);
expr7=(pow(q-a,2)+pow(p,2))*pow(q+a,2)-pow(c7,4);
expr8=(pow(q-a,2)+pow(p,2))*pow(q+a,2)-pow(c8,4);
expr9=(pow(q-a,2)+pow(p,2))*pow(q+a,2)-pow(c9,4);
courbe1=(abs(expr1)<e1);
courbe2=(abs(expr2)<e2);
courbe3=(abs(expr3)<e3);
courbe4=(abs(expr4)<e4);
courbe5=(abs(expr5)<e5);
courbe6=(abs(expr6)<e6);
courbe7=(abs(expr7)<e7);
courbe8=(abs(expr8)<e8);
courbe9=(abs(expr9)<e9);
green=1-0.5*(courbe1||courbe2||courbe3||courbe4||courbe5||courbe6||courbe7);
blue=1-0.5*(courbe2||courbe3||courbe4||courbe5||courbe6||courbe7||courbe8);
red=1-0.5*(courbe3||courbe4||courbe5||courbe6||courbe7||courbe8||courbe9);

 34courbeplane31.jpg

4 : Ovale de Cassini

41 : Neuf ovales

L'ovale de Cassini a pour équation ((x - a)^2 + y^2)((x +a)^2 + y^2) - b^4 = 0.

Quatre cas : b < a , b = a , a < b < a*sqrt(2) , b >= a*sqrt(2)

Formule fond (ou texture) Rendu

a=1;
b1=0.25*a;b2=0.5*a;b3=a;b4=1.09*a;b5=1.19*a;b6=1.3*a;b7=1.41*a;b8=2.82*a;b9=5.64*a;
e1=0.01;e2=0.01;e3=0.1;e4=0.1;e5=0.1;e6=0.1;e7=0.1;e8=0.1;e9=0.1;
pmin=-2;pmax=2;
qmin=-2;qmax=2;
p=(pmax-pmin)*u+pmin;
q=(qmax-qmin)*v+qmin;
expr1=(pow(p-a,2)+pow(q,2))*(pow(p+a,2)+pow(q,2))-pow(b1,4);
expr2=(pow(p-a,2)+pow(q,2))*(pow(p+a,2)+pow(q,2))-pow(b2,4);
expr3=(pow(p-a,2)+pow(q,2))*(pow(p+a,2)+pow(q,2))-pow(b3,4);
expr4=(pow(p-a,2)+pow(q,2))*(pow(p+a,2)+pow(q,2))-pow(b4,4);
expr5=(pow(p-a,2)+pow(q,2))*(pow(p+a,2)+pow(q,2))-pow(b5,4);
expr6=(pow(p-a,2)+pow(q,2))*(pow(p+a,2)+pow(q,2))-pow(b6,4);
expr7=(pow(p-a,2)+pow(q,2))*(pow(p+a,2)+pow(q,2))-pow(b7,4);
expr8=(pow(p-a,2)+pow(q,2))*(pow(p+a,2)+pow(q,2))-pow(b8,4);
expr9=(pow(p-a,2)+pow(q,2))*(pow(p+a,2)+pow(q,2))-pow(b9,4);
courbe1=(abs(expr1)<e1);
courbe2=(abs(expr2)<e2);
courbe3=(abs(expr3)<e3);
courbe4=(abs(expr4)<e4);
courbe5=(abs(expr5)<e5);
courbe6=(abs(expr6)<e6);
courbe7=(abs(expr7)<e7);
courbe8=(abs(expr8)<e8);
courbe9=(abs(expr9)<e9);
green=1-0.9*(courbe1||courbe2||courbe3);
blue=1-0.9*(courbe7||courbe8||courbe9);
red=1-0.9*(courbe4||courbe5||courbe6);

 34courbeplane41.jpg

5 : Trisectrice de Ceva

La trisectrice de Ceva a pour équation cartésienne (x^2 + y^2)^3 - a^2 (3 x^2 - y^2)^2 et pour équation polaire rho = a*(4*cos(t)^2 - 1)

On la représente dans le plan z = c

D'où sa paramétrisation spatiale (x = rho*cos(t) , y = rho*sin(t) , z = c).

51 : Représentation spatiale sous forme de courbe plane

Formule objet Formule texture Rendu  

a=2;c=0;
p=2*PI*u;
q=2*PI*v;
t=p+q;
rho=a*(4*pow(cos(t),2)-1);
x=rho*cos(t);
y=rho*sin(t);
z=c;

 mt=8;
p=2*PI*u;
red=abs(cos(mt*p));
blue=abs(cos(mt*p+2*PI/3));
green=abs(cos(mt*p+4*PI/3));		 34courbeplane51.jpg 34courbeplane501.jpg

52 : Représentation spatiale sous forme de courbe spatiale (fonction writhe)

Si M(t) = (f(t) , g(t)) est la paramétrisation d'une courbe plane, on note writhe(M(t)) la courbe spatiale (f(t) , g(t)*cos(t) , g(t)*sin(t))

Le coefficient e, avec e >= 1, permet de construire plus de points (plusieurs tours) donc d'épaissir le trait.

Formule objet Formule texture Rendu

a=2;e=2;
t=e*PI*(u+v);
rho=a*(4*pow(cos(t),2)-1);
x=rho*cos(t);
y=rho*sin(t)*cos(t);
z=rho*sin(t)*sin(t);

 mt=8;
p=2*PI*u;
red=abs(cos(mt*p));
blue=abs(cos(mt*p+2*PI/3));
green=abs(cos(mt*p+4*PI/3));		 34courbeplane52.jpg

53 : Représentation spatiale sous forme de surface de révolution

Formule objet Formule texture Rendu

a=2;
p=2*PI*u;
q=PI*v;
rho=a*(4*pow(cos(p),2)-1);
x=rho*cos(p);
y=rho*sin(p)*cos(q);
z=rho*sin(p)*sin(q);

 mt=8;
q=2*PI*v;
red=abs(cos(mt*q));
green=abs(cos(mt*q+2*PI/3));
blue=abs(cos(mt*q+4*PI/3));		 34courbeplane53.jpg

6 : Hypotrochoïde

Étant donnés deux cercles (Ca) et (Cb) de rayons respectifs a et b tels que b < a et étant donné un point M lié au cercle (Cb), on appelle hypotrochoïde le lieu des points M tels que le cercle (Cb) roule sans glisser sur le cercle (Ca), intérieurement à ce dernier. On note d la distance du point M au centre du cercle (Cb) et soit s= a/b - 1.

L'hypotrochoïde a alors pour paramétrisation (x = b*s*cos(t) + d*cos(s*t) , y = b*s*sin(t) -d*sin(s*t).

On représente l'hypotrochoïde dans le plan z = c

Cinq cas peuvent être considérés : 0 < d < b , d = b (hypocycloïde) , b < d < b*s , d = b*s (rosace) , d > b*s

Le coefficient e, avec e >= 1, permet de construire plus de points (plusieurs tours) donc d'épaissir le trait.

60 :

34courbeplane601.jpg

 34courbeplane602.jpg

61 : b = 1 , s = 4 et d = 0.5

Formule objet Formule texture Rendu

b=1;s=4;d=0.5;c=0;e=3;
t=e*PI*(u+v);
x=b*s*cos(t)+d*cos(s*t);
y=b*s*sin(t)-d*sin(s*t);
z=c;

 mt=55;
p=2*PI*u;
red=abs(cos(mt*p));
blue=abs(cos(mt*p+2*PI/3));
green=abs(cos(mt*p+4*PI/3));		 34courbeplane61.jpg

62 : b = 1 , s = 4 et d = 1

Formule objet Formule texture Rendu

b=1;s=4;d=1;c=0;e=2.5;
t=e*PI*(u+v);
x=b*s*cos(t)+d*cos(s*t);
y=b*s*sin(t)-d*sin(s*t);
z=c;

 mt=55;
p=2*PI*u;
red=abs(cos(mt*p));
blue=abs(cos(mt*p+2*PI/3));
green=abs(cos(mt*p+4*PI/3));		 34courbeplane62.jpg

63 : b = 1 , s = 4 et d = 2.5

Formule objet Formule texture Rendu

b=1;s=4;d=2.5;c=0;e=1.5;
t=e*PI*(u+v);
x=b*s*cos(t)+d*cos(s*t);
y=b*s*sin(t)-d*sin(s*t);
z=c;

 mt=55;
p=2*PI*u;
red=abs(cos(mt*p));
blue=abs(cos(mt*p+2*PI/3));
green=abs(cos(mt*p+4*PI/3));		 34courbeplane63.jpg

64 : b = 1 , s = 4 et d = 4

Formule objet Formule texture Rendu

b=1;s=4;d=4;c=0;e=1.2;
t=e*PI*(u+v);
x=b*s*cos(t)+d*cos(s*t);
y=b*s*sin(t)-d*sin(s*t);
z=c;

 mt=55;
p=2*PI*u;
red=abs(cos(mt*p));
blue=abs(cos(mt*p+2*PI/3));
green=abs(cos(mt*p+4*PI/3));		 34courbeplane64.jpg

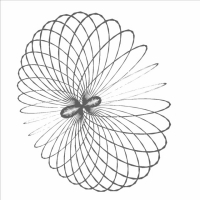
65 : b = 1 , s = 4 et d = 5

Formule objet Formule texture Rendu

b=1;s=4;d=5;c=0;e=1;
t=e*PI*(u+v);
x=b*s*cos(t)+d*cos(s*t);
y=b*s*sin(t)-d*sin(s*t);
z=c;

 mt=55;
p=2*PI*u;
red=abs(cos(mt*p));
blue=abs(cos(mt*p+2*PI/3));
green=abs(cos(mt*p+4*PI/3));		 34courbeplane65.jpg

7 : Épitrochoïde

Étant donnés deux cercles (Ca) et (Cb) de rayons respectifs a et b tels que et étant donné un point M lié au cercle (Cb), on appelle épitrochoïde le lieu des points M tels que le cercle (Cb) roule sans glisser sur le cercle (Ca), extérieurement à ce dernier. On note d la distance du point M au centre du cercle (Cb) et soit s= a/b +1.

L'épitrochoïde a alors pour paramétrisation (x = b*s*cos(t) -d*cos(s*t) , y = b*s*sin(t) -d*sin(s*t).

On représente l'hypotrochoïde dans le plan z = c

Cinq cas peuvent être considérés : 0 < d < b , d = b (épicycloïde) , b < d < b*s , d = b*s (rosace) , d > b*s

Le coefficient e, avec e >= 1, permet de construire plus de points (plusieurs tours) donc d'épaissir le trait.

71 : Représentation spatiale

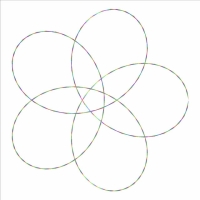
71 : b = 1 , s = 6 et d = 0.5

Formule objet Formule texture Rendu

b=1;s=6;d=0.5;c=0;e=2.5;
t=e*PI*(u+v);
x=b*s*cos(t)-d*cos(s*t);
y=b*s*sin(t)-d*sin(s*t);
z=c;

 mt=55;
p=2*PI*u;
red=abs(cos(mt*p));
blue=abs(cos(mt*p+2*PI/3));
green=abs(cos(mt*p+4*PI/3));		 34courbeplane71.jpg

72 : b = 1 , s = 6 et d = 1

Formule objet Formule texture Rendu

b=1;s=6;d=1;c=0;e=2;
t=e*PI*(u+v);
x=b*s*cos(t)-d*cos(s*t);
y=b*s*sin(t)-d*sin(s*t);
z=c;

 mt=55;
p=2*PI*u;
red=abs(cos(mt*p));
blue=abs(cos(mt*p+2*PI/3));
green=abs(cos(mt*p+4*PI/3));		 34courbeplane72.jpg

73 : b = 1 , s = 6 et d = 3.5

Formule objet Formule texture Rendu

b=1;s=6;d=3.5;c=0;e=1;
t=e*PI*(u+v);
x=b*s*cos(t)-d*cos(s*t);
y=b*s*sin(t)-d*sin(s*t);
z=c;

 mt=55;
p=2*PI*u;
red=abs(cos(mt*p));
blue=abs(cos(mt*p+2*PI/3));
green=abs(cos(mt*p+4*PI/3));		 34courbeplane73.jpg

74 : b = 1 , s = 6 et d = 6

Formule objet Formule texture Rendu

b=1;s=6;d=6;c=0;e=1;
t=e*PI*(u+v);
x=b*s*cos(t)-d*cos(s*t);
y=b*s*sin(t)-d*sin(s*t);
z=c;

 mt=55;
p=2*PI*u;
red=abs(cos(mt*p));
blue=abs(cos(mt*p+2*PI/3));
green=abs(cos(mt*p+4*PI/3));		 34courbeplane74.jpg

75 : b = 1 , s = 6 et d = 7

Formule objet Formule texture Rendu

b=1;s=6;d=7;c=0;e=1;
t=e*PI*(u+v);
x=b*s*cos(t)-d*cos(s*t);
y=b*s*sin(t)-d*sin(s*t);
z=c;

 mt=55;
p=2*PI*u;
red=abs(cos(mt*p));
blue=abs(cos(mt*p+2*PI/3));
green=abs(cos(mt*p+4*PI/3));		 34courbeplane75.jpg

8 : Diverses courbes

81 : Astroïde, deux trifoliums et un cercle

Les deux trifoliums ont pour équations respectives (x^2 + y^2)^2 - a*x*(x^2 - 3*y^2) = 0 et (x^2 + y^2)^2 +a*x*(x^2 - 3*y^2) = 0 , le deuxième étant symétrique du premier par rapport à l'axe des ordonnées.

L'astroïde, après rotation de centre l'origine du repère et d'angle PI/4, a pour équation ((sqrt(2)/2)*(x + y)^(2/3) + ((sqrt(2)/2)*(-x +y)^(2/3) - b^(2/3) = 0

(au lieu de x^(2/3) + y^(2/3) - b^(2/3) = 0, équation habituelle)

Le cercle a pour équation x^2 + y^2 - a^2 = 0

Formule fond (ou texture) Rendu
a=1;b=2*a;
e=0.01;
pmin=-1.5;pmax=1.5;
qmin=-1.5;qmax=1.5;
p=(pmax-pmin)*u+pmin;
q=(qmax-qmin)*v+qmin;
expr1=pow(p*p+q*q,2)-a*p*(p*p-3*q*q);
expr2=pow(p*p+q*q,2)+a*p*(p*p-3*q*q);
expr3=p*p+q*q-a*a;
expr4=pow(0.5*pow(p+q,2),1/3)+pow(0.5*pow(-p+q,2),1/3)-pow(b*b,1/3);
courbe1=(abs(expr1)<e);
courbe2=(abs(expr2)<e);
courbe3=(abs(expr3)<e);
courbe4=(abs(expr4)<e);
red=1-0.2*(courbe1||courbe2);
blue=1-0.7*(courbe2||courbe3);
green=1-0.5*(courbe3||courbe1||courbe4);		 34courbeplane81.jpg